Given a Square with vertices (0, 0) (L, 0) (L, L) (0, L,). A small (point size) ball is thrown with initial velocity v from (0, 0).
Every collision follows following constraints:
- After collision, the magnitude of velocity either doubles (with probability p) or halves(with probability 1-p).
- For every collision, angle of incidence is equal to angle of reflection irrespective of the change in magnitude of velocity.
- On collsion with corner, the ball will retrace it's path.
You need to calculate the expected time after which the ball first intersects or retraces it's own trajectory.
Input:
Single line containing five space separated integers L Vx Vy P Q
L = Side length of square
Vx = Horizontal component of velocity
Vy = Vertical component of velocity
p (probability of mangitude of velocity being doubled) = P/Q
Output:
Single integer, expected time modulo 109+7
Constraints:
- 1 ≤ L,Q ≤ 109
- 0 ≤ P,Vx,Vy ≤ 109
- 0 ≤ max(Vx,Vy)
- P ≤ Q
- (L*Vx)/Vy is an integer
4 1 2 1 2
500000008
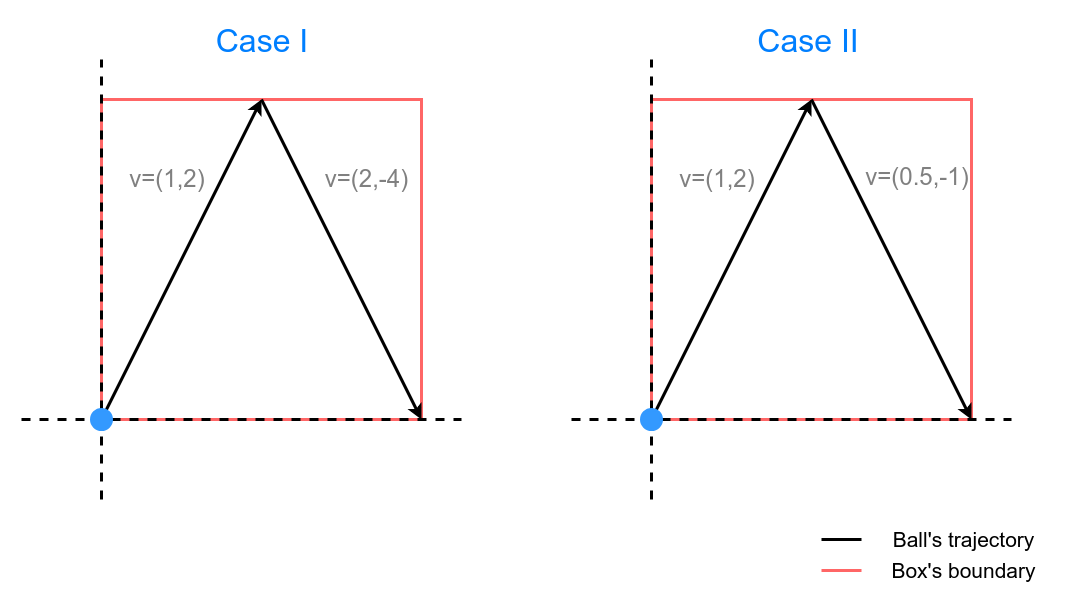
Total time for case I: 2 + 1 = 3
Total time for case II: 2 + 4 = 6
Expected time = (3 + 6)/2 = 9/2 = 500000008 modulo 1000000007
Please login to use the editor
You need to be logged in to access the code editor
Loading...
Please wait while we load the editor
Login to unlock the editorial
Please login to use the editor
You need to be logged in to access the code editor
Loading...
Please wait while we load the editor